React 和 D3 实现簇布局2019-03-29Θ
相关知识#
工作原理#
使用的是 D3 cluster layout 中的 API,对简单的数据进行格式化,补充父级、子级、坐标位置(Automatic Graph Drawing 算法)等可用数据。同时,提供快捷函数拿到需要数据进行渲染绘图。渲染后的数据结构如下:
{children: Array, // 子级data: Object, // 自身数据depth: Number,height: Number,parent: Object, // 父级x: Number, // x 轴坐标y: Number, // y 轴坐标}
使用函数#
- d3.layout.cluster() 设置默认簇布局
- d3.layout.hierarchy() 默认设置创建新的分层布局
- root.descendants() 所有节点的数组
- root.links() 表达父子关系的数组
实现简单的簇布局#
依赖 d3-hierarchy
<ClusterLayout/>
import React from 'react';import { hierarchy, cluster } from 'd3-hierarchy';import data from './datas';import './style.scss';const width = 450;const height = 500;const clusterLayout = cluster().size([height - 50, width - 100]);const root = hierarchy(data, function (d) {return d.children;});clusterLayout(root);class ClusterLayout extends React.PureComponent {renderNodes = () => {return root.descendants().map((d, idx) => {return (<gclassName="node"key={`link_${idx}`}><circle r="4" cx={d.x} cy={d.y}/></g>)});}renderLinks = () => {return root.links().map((d, idx) => {return (<lineclassName="link"key={`link_${idx}`}x1={d.source.x}y1={d.source.y}x2={d.target.x}y2={d.target.y}/>)});}renderSvg = () => {return (<svg width={width} height={height}><g transform="translate(0, 40)"><g className="links">{this.renderLinks()}</g><g className="nodes">{this.renderNodes()}</g></g></svg>)}render() {return (<div className="Dendrogram">{this.renderSvg()}</div>)}}export default ClusterLayout;
绘制曲线#
绘制曲线链接需要将 line 改为更加灵活的 path 进行绘图。改动细节:
// 格式化function formatPath(d) {const averageX = (d.source.x + d.target.x) / 2;return `M ${d.source.x}, ${d.source.y}C ${averageX}, ${d.source.y} ${averageX}, ${d.target.y} ${d.target.x}, ${d.target.y}`;}// 使用 pathrenderLinks = () => {return root.links().map((d, idx) => {return (<pathclassName="link"d={formatPath(d)}key={`link_${idx}`}/>)});}
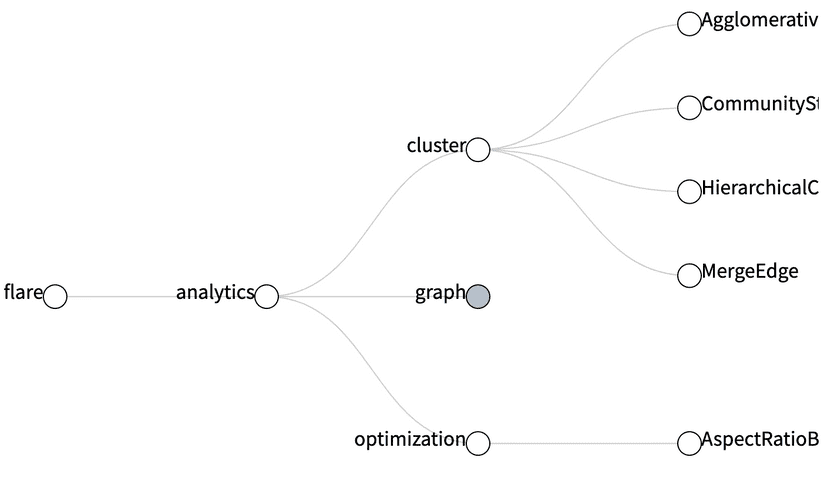
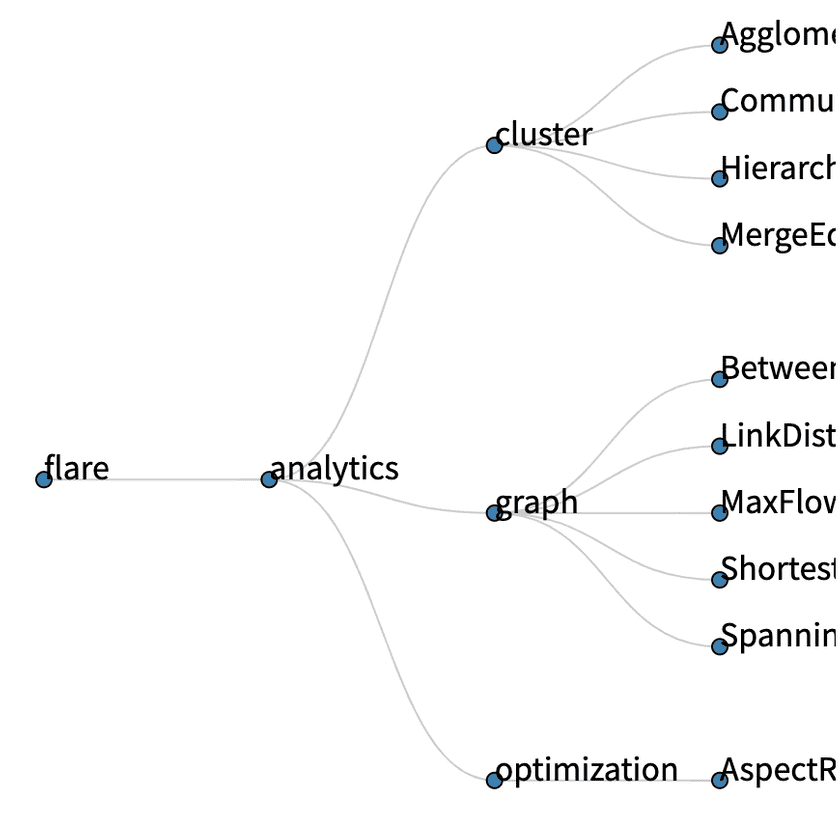
横向排列并补充文案#
- 线条:要将 formatPath 函数的 x、y 对换
- 节点:transform 翻转,同时去掉 circle 的 cx、cy 属性
// 线条 x、y 轴对换function formatPath(d) {const averageY = (d.source.y + d.target.y) / 2;return `M ${d.source.y}, ${d.source.x}C ${averageY}, ${d.source.x} ${averageY}, ${d.target.x} ${d.target.y}, ${d.target.x}`;}// 节点翻转renderNodes = () => {return root.descendants().map((d, idx) => {return (<gtransform={`translate(${d.y}, ${d.x})`}className="node"key={`link_${idx}`}><circle r="4" /><text>{d.data.name}</text></g>)});}
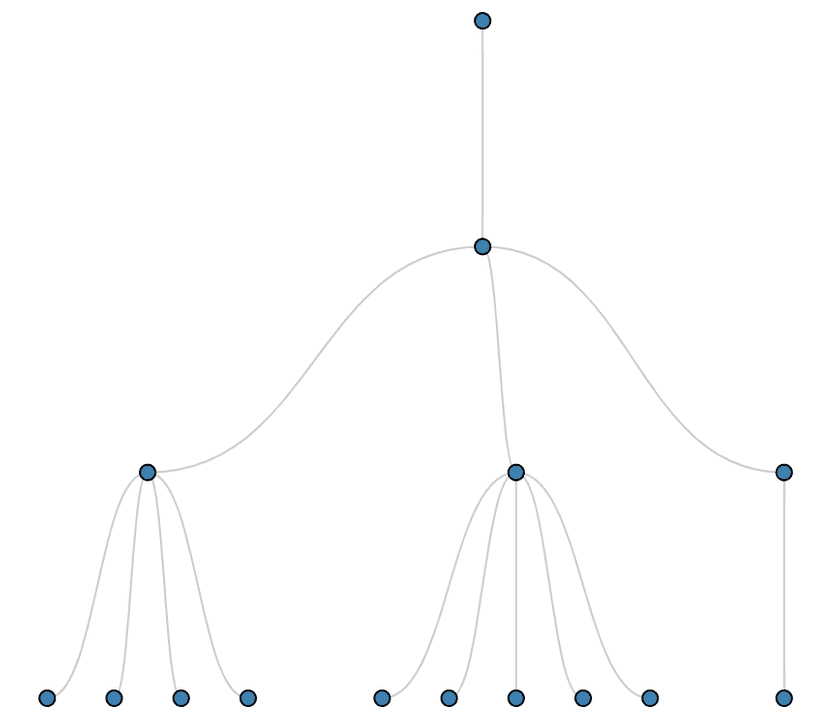
实现收缩#
CollapsibleTree
import React from 'react';import { hierarchy, cluster } from 'd3-hierarchy';import { select } from 'd3-selection';import datas from './datas';import './style.scss'// Set the dimensions and margins of the diagramconst width = 700;const height = 500;const diameter = 10;const distance = 160;// Collapse the node and all it's childrenfunction collapse(d) {if (d.children) {d._children = d.childrend._children.forEach(collapse)d.children = null}}// Creates a curved (diagonal) path from parent to the child nodesfunction diagonal(s, d) {const averageY = (s.y + d.y) / 2;return `M ${s.y}, ${s.x}C ${averageY}, ${s.x} ${averageY}, ${d.x} ${d.y}, ${d.x}`;}const clusterLayout = cluster().size([height, width - 100]);// Assigns parent, children, height, depthconst root = hierarchy(datas, function (d) { return d.children; });root.x0 = height / 2;root.y0 = 0;class CollapsibleTree extends React.PureComponent {componentDidMount() {const svg = select('.CollapsibleTree svg g');let i = 0;// Collapse after the second levelroot.children.forEach(collapse);update(root);function update(source) {// Assigns the x and y position for the nodesconst treeData = clusterLayout(root);// Compute the new tree layout.const nodes = treeData.descendants();const links = treeData.descendants().slice(1);nodes.forEach(function (d) { d.y = d.depth * distance });// Update the nodes...const node = svg.selectAll('g.node').data(nodes, function (d) { return d.id || (d.id = ++i); });// Enter any new modes at the parent's previous position.const nodeEnter = node.enter().append('g').attr('class', 'node').attr("transform", function (d) {return "translate(" + source.y0 + "," + source.x0 + ")";}).on('click', click);// Add Circle for the nodesnodeEnter.append('circle').attr('class', 'node').attr('r', diameter).style("fill", function (d) {return d._children ? "lightsteelblue" : "#fff";});// Add labels for the nodesnodeEnter.append('text').attr("dy", 2).attr("x", function (d) {return d.children || d._children ? -diameter : diameter;}).attr("text-anchor", function (d) {return d.children || d._children ? "end" : "start";}).text(function (d) { return d.data.name; });// UPDATEconst nodeUpdate = nodeEnter.merge(node);// Transition to the proper position for the nodenodeUpdate.attr("transform", function (d) {return "translate(" + d.y + "," + d.x + ")";});// Update the node attributes and stylenodeUpdate.select('circle.node').attr('r', 10).style("fill", function (d) {return d._children ? "lightsteelblue" : "#fff";}).attr('cursor', 'pointer');// Remove any exiting nodesnode.exit().attr("transform", function (d) {return "translate(" + source.y + "," + source.x + ")";}).remove();// Update the links...const link = svg.selectAll('path.link').data(links, function (d) { return d.id; });// Enter any new links at the parent's previous position.const linkEnter = link.enter().insert('path', "g").attr("class", "link").attr('d', function (d) {const o = { x: source.x0, y: source.y0 }return diagonal(o, o)});// UPDATEconst linkUpdate = linkEnter.merge(link);// Transition back to the parent element positionlinkUpdate.attr('d', function (d) { return diagonal(d, d.parent) });// Remove any exiting linkslink.exit().attr('d', function (d) {const o = { x: source.x, y: source.y }return diagonal(o, o)}).remove();// Store the old positions for transition.nodes.forEach(function (d) {d.x0 = d.x;d.y0 = d.y;});// Toggle children on click.function click(d) {if (d.children) {d._children = d.children;d.children = null;} else {d.children = d._children;d._children = null;}update(d);}}}render() {return (<div className="CollapsibleTree"><svg width={width} height={height}><g transform="translate(50, 0)"/></svg></div>)}}export default CollapsibleTree;
参考#
- Automatic Graph Drawing 算法: tidier-drawings, buchheim improving
- D3 Wiki 簇布局
- 实践:dendrogram_basic
- d3-hierarchy
- d3-selection